※ ANOVA Test(ANalysis Of VAriance; 분산 분석)이란
- 분산분석(ANOVA; 변량 분석)은 3개 이상 다수의 집단을 비교할 때 사용하는 가설검정법
= 여러 그룹간의 평균의 차이가 통계적으로 유의미 한지를 판단하기 위한 시험법 - ANOVA와 T-Test의 차이점
- ANOVA Test : 3개 이상의 그룹의 평균을 비교하는 데 사용
- T - Test : 2개의 그룹을 비교하는 데 사용
( 다수 집단 비교에서 t-test를 여러번 사용하면, 다중검정문제 발생으로 1종 오류가 증가하게 됨 )
-> 따라서, 다수 간의 평균 비교에서 ANOVA를 통해 유의한 차이를 검정 - 그룹은 분산을 분석하여 추론한 차이를 의미
- ANOVA는 분산 기반 F 테스트를 사용하여 그룹 평균 동등성을 확인
- ANOVA F 테스트는 비특이적 귀무 가설을 테스트하기 때문에 옴니버스 테스트라고도 함.
즉, 모든 그룹 평균이 동일함. - 주요 유형: 1요인 및 2요인 ANOVA(요인은 독립변수임)
- 동일한 피험자에 대한 치료 또는 시간에 대해 반복 측정 이 있는 경우 반복 측정 ANOVA 를 사용해야 한다.
- 정리 : 분산분석(ANOVA)는 전체 그룹간의 평균값 차이가 통계적 의미가 있는지 판단하는데 유용한 도구이다.
그러나 정확히 어느 그룹의 평균값이 의미가 있는지는 알려주지 않기때문에 추가적인 사후분석(Post Hoc Analysis) 이 필요하다.
(참고: ANOVA에서 그룹, 요인 및 독립 변수는 유사한 용어임.)
※ 분산 분석의 종류
1) 일원 분산분석(One-way ANOVA)
- '독립변인 1개' and '종속변인 1개'일 때, 집단 간의 유의미한 차이 검정
ex) 한/중/일 국가간 학습기술에 따른 성적비교 (독립변인 : 학습기술)

2) 이원 분산분석(Two-way ANOVA)
- '독립변인 2개' and '종속변인 1개'일 때, 집단 간의 유의미한 차이 검정
ex) 한/중/일 국가간 성별과 운동량에 따른 체중비교 ( 독립변인 : 성별 / 운동량 )

3) 다원변량 분산분석(MANOVA;multiple analysis of cariance)
- '독립변인 1개' and '종속변인 2개'일 때, 집단 간의 유의미한 차이 검정 (One-way MANOVA)

- '독립변인 2개' and '종속변인 2개'일 때, 집단 간의 유의미한 차이 검정 (Two-way MANOVA)

4) 공 분산분석(ANCOVA; analysis of covariance)
- 특정한 독립변인을 중점에 두고, 나머지 독립변인은 공변량(Covariates)로 분석하는 방법

※ ANOVA의 3가지 조건
- 정규성 : 각각의 그룹에서 변인은 정규분포.
- 분산의 동질성 : Y의 모집단 분산은 각각의 모집단에서 동일.
- 관찰의 독립성: 각각의 모집단에서 크기가 각각인 표본들이 독립적으로 표집.
※ 분산(variance)의 중요성
- 아래의 두개의 그림을 통해 분산에 대해 알아보면, 평균값은 동일하지만
분산 값이 다름으로 인해 전체적인 데이터의 모습이 완전히 달라 보이는것을 알 수 있다.

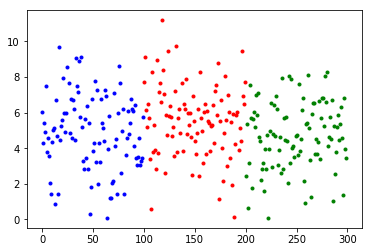
- 이것을 통해 알 수 있는 두 가지.
1. 집단 평균값 의 분산이 클수록 그리고,
2. 집단 내 분산이 작아질수록 평균의 차이가 분명해진다.
집단 간 분산과 집단 내 분산 이 두가지를 이용해 분석을 하기에 분산분석이라고 한다.
분산분석에는 여러 종류가 있지만, 여기서는 일원분산분석(One-way ANOVA)과 이원분산분석(Two-way ANOVA)를 알아보려한다.
(1) 일원분산분석(One-way ANOVA)
종속변인은 1개이며, 독립변인의 집단도 1개인 경우이다.
한가지 변수의 변화가 결과 변수에 미치는 영향을 보기 위해 사용된다.
파이썬에서 One-way ANOVA 분석은 scipy.stats이나 statsmodel 라이브러리를 이용해서 할 수 있다.
statsmodel 라이브러리가 좀 더 많고 규격화된 정보를 제공합니다.
예시 데이터(Altman 910) 설명
22명의 심장 우회 수술을 받은 환자를 다음의 3가지 그룹으로 나누었습니다.
- Group I: 50% 아산화 질소(nitrous oxide)와 50%의 산소(oxygen) 혼합물을 24시간 동안 흡입한 환자
- Group II: 50% 아산화 질소와 50% 산소 혼합물을 수술 받는 동안만 흡입한 환자
- Group III: 아산화 질소 없이 오직 35-50%의 산소만 24시간동안 처리한 환자
그런 다음 적혈구의 엽산 수치를 24시간 이후에 측정하였습니다.
# url로 데이터 얻어오기
url = 'https://raw.githubusercontent.com/thomas-haslwanter/statsintro_python/master/ipynb/Data/data_altman/altman_910.txt'
data = np.genfromtxt(urllib.request.urlopen(url), delimiter=',')
# 구분자가 쉼표로 된 파일을 불러옴
# Sort them into groups, according to column 1
group1 = data[data[:,1]==1,0]
group2 = data[data[:,1]==2,0]
group3 = data[data[:,1]==3,0]
# matplotlib plotting
plot_data = [group1, group2, group3]
ax = plt.boxplot(plot_data)
plt.show()
Boxplot에서 볼 수 있듯이, 평균값의 차이가 실제로 의미가 있는 차이인지, 분산이 커서 그런것인지 애매한 상황.
이런 상황에서 분산분석을 통해 통계적 유의성을 알아 볼 수 있다.
(1-1) Scipy.stats으로 일원분산분석
아래와 같은 간단한 코드로 분산분석을 할 수 있음.
F_statistic, pVal = stats.f_oneway(group1, group2, group3)
print('Altman 910 데이터의 일원분산분석 결과 : F={0:.1f}, p={1:.5f}'.format(F_statistic, pVal))
if pVal < 0.05:
print('P-value 값이 충분히 작음으로 인해 그룹의 평균값이 통계적으로 유의미하게 차이남.')이번에는 좀 더 다양한 방법으로 pandas와 statsmodels 라이브러리를 사용해서 분산분석해보려 함.
(1-2) Statsmodel을 사용한 일원분산분석 (OLS 회귀분석-선형최소적합)
전처리한 자료에 회귀분석을 적용해 변수별 회귀계수를 구할 수 있다.
(목적 - 종속변수라고 불리는 변수집합과 설명변수라고 불리는 또 다른 집합변수 사이관계를 기술하는 것)
( 단순회귀 : 설명변수 하나, 종속변수 하나
다중회귀 : 설명변수 다수, 종속변수 하나
다변량회귀 : 종속변수가 하나 이상 )
import statsmodels.api as sm
import statsmodels.formula.api as smf
# 경고 메세지 무시하기
import warnings
warnings.filterwarnings('ignore')
df = pd.DataFrame(data, columns=['value', 'treatment'])
# the "C" indicates categorical data
model = ols('value ~ C(treatment)', df).fit()
print(anova_lm(model))

보시다시피 statsmodels 을 사용하면 보다 간편하면서도 깔끔한 결과를 얻을 수 있다.
(2) 이원분산분석(two-way ANOVA)
독립변인의 수가 두 개 이상일 때 집단 간 차이가 유의한지를 검증하는 데 사용한다.
상호작용효과(Interaction effect), 한 변수의 변화가 결과에 미치는 영향이 다른 변수의 수준에 따라 달라지는지를
확인하기 위해 사용된다.
예제 데이터(altman_12_6) 설명
태아의 머리 둘레 측정 데이터( 4명의 관측자가 3명의 태아를 대상으로 측정을 함)
이를 통해서 초음파로 태아의 머리 둘레측정 데이터가 재현성이 있는지를 조사하였다.
inFile = 'altman_12_6.txt'
url_base = 'https://raw.githubusercontent.com/thomas-haslwanter/statsintro_python/master/ipynb/Data/data_altman/'
url = url_base + inFile
data = np.genfromtxt(urllib.request.urlopen(url), delimiter=',')
# Bring them in dataframe-format
df = pd.DataFrame(data, columns=['head_size', 'fetus', 'observer'])
# df.tail()
# 태아별 머리 둘레 plot 만들기
df.boxplot(column = 'head_size', by='fetus' , grid = False)>>> <matplotlib.axes._subplots.AxesSubplot at 0xb21b748>
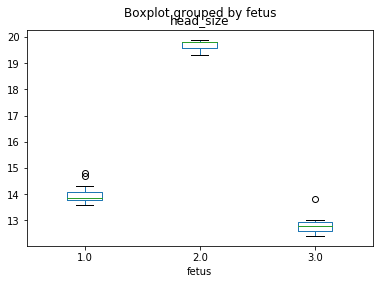
그림을 보니 태아(fetus) 3명의 머리 둘레는 차이가 있어보이나,
이것이 관측자와 상호작용이 있는것인지 분석을 통해 알아 볼 예정.
분산분석으로 상관관계
statmodels 라이브러리를 사용해 간단하게 계산할 수 있다.
formula = 'head_size ~ C(fetus) + C(observer) + C(fetus):C(observer)'
lm = ols(formula, df).fit()
print(anova_lm(lm))
P-value 가 0.05 이상, 따라서 귀무가설을 기각할 수 없고. 측정자와 태아의 머리둘레값에는 연관성이 없다고 할 수 있다.
측정하는 사람이 달라도 머리 둘레값은 일정한 것 /
=> 결론적으로 초음파로 측정하는 태아의 머리둘레값은 믿을 수 있다는 것
※ ANOVA 가설
- 귀무 가설 : 그룹 평균이 동일함(그룹 평균에 변동 없음)
H 0 : μ 1 =μ 2 =…=μ p - 대립 가설 : 적어도 하나의 그룹 평균은 다른 그룹과 다릅니다
H 1 : 모든 μ가 같지 않음
※ ANOVA 가정
- 잔차(실험 오차)는 대략적으로 정규 분포를 따릅니다(Shapiro-Wilks 검정 또는 히스토그램).
- 등분산성 또는 분산의 동질성(처리 그룹 간에 분산이 같음)(Levene 또는 Bartlett의 검정)
- 관찰은 서로 독립적으로 샘플링된다.(그룹 간 및 그룹 내 관찰과 관련 없음).
즉, 각 대상에는 하나의 응답만 있어야 한다.
※ ANOVA가 어떻게 작동하는지
- 표본 크기 확인: 각 그룹에서 동일한 수의 관측치
- 각 그룹에 대한 평균 제곱(MS) 계산(그룹/레벨-1의 SS); level-1은 그룹의 자유도(df)입니다.
- 평균 제곱 오차(MSE) 계산(SS 오차/잔차 df)
- F 값 계산 (그룹의 MS/MSE)
- F 값과 자유도(df)를 기반으로 p 값 계산
출처 - https://partrita.github.io/posts/ANOVA-python/



